| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 3.1 | Example 1 & 2 (Before Exercise 3.2) | Exercise 3.2 |
Chapter 3 Coordinate Geometry
Welcome to the solutions guide for Chapter 3, "Coordinate Geometry," from the latest Class 9 NCERT mathematics textbook prescribed for the academic session 2024-25. This fundamental chapter introduces the powerful system developed by René Descartes for precisely locating points in a two-dimensional plane, thereby creating a crucial bridge between algebra and geometry. Mastering the concepts presented here is essential for visualizing functions, graphing equations, and understanding various geometric representations throughout mathematics and science. These solutions provide clear, concise explanations and step-by-step guidance for all exercises, ensuring a solid grasp of the Cartesian coordinate system.
The core of this chapter revolves around understanding the structure and terminology of the Cartesian Coordinate System. The solutions thoroughly explain its key components: two perpendicular number lines intersecting at a point. These are:
- The horizontal line, designated as the x-axis.
- The vertical line, designated as the y-axis.
- The point of intersection of these axes, known as the Origin, which represents the zero point $(0, 0)$ on both lines.
A central concept is the representation of any point in the plane using an ordered pair of numbers, $(x, y)$, known as its coordinates. The solutions explicitly define:
- The abscissa, or x-coordinate, which represents the perpendicular distance of the point from the y-axis (measured along the x-axis).
- The ordinate, or y-coordinate, which represents the perpendicular distance of the point from the x-axis (measured along the y-axis).
The practical skills developed in this chapter involve plotting and reading points. The solutions provide clear, step-by-step instructions for plotting points when their coordinates $(x, y)$ are given. This involves starting at the origin, moving $x$ units horizontally along the x-axis (right for positive $x$, left for negative $x$), and then moving $y$ units vertically parallel to the y-axis (up for positive $y$, down for negative $y$) to locate the point accurately. Conversely, the solutions guide students on how to read the coordinates of a point already marked on the Cartesian plane by determining its perpendicular distances from the y-axis (to find $x$) and the x-axis (to find $y$), paying attention to the signs based on the quadrant or axis.
Furthermore, the solutions address exercises that require identifying the specific quadrant in which a point lies based solely on the signs of its abscissa and ordinate (e.g., $(+, +)$ in Q-I, $(-, +)$ in Q-II, $(-, -)$ in Q-III, $(+, -)$ in Q-IV). They also clarify the characteristics of points lying on the axes themselves: points on the x-axis always have an ordinate of 0 (form $(x, 0)$), and points on the y-axis always have an abscissa of 0 (form $(0, y)$).
Regarding the rationalized syllabus for 2024-25, Chapter 3, "Coordinate Geometry," in the Class 9 NCERT textbook remains largely unchanged as it covers fundamental concepts. The rationalization process did not remove any significant topics from this concise chapter. By utilizing these solutions, students can achieve precision in understanding the coordinate system's terminology and master the essential skills of plotting and interpreting points, establishing a vital foundation for future graphical work in mathematics.
Exercise 3.1
Question 1. How will you describe the position of a table lamp on your study table to another person?
Answer:
To describe the position of a table lamp on a study table to another person, we can use a method similar to locating a point on a plane using coordinates. We can consider the study table as a flat surface (a plane) and use two perpendicular edges of the table as reference lines or axes.
Here is how you can describe the position:
Step 1: Choose Reference Lines
Imagine the study table as a coordinate plane. Choose two adjacent edges of the rectangular study table that meet at a corner. Let's say you choose the left edge and the front edge.
Consider the left edge as the y-axis and the front edge as the x-axis. The corner where these two edges meet can be considered as the origin (0,0).
Step 2: Measure Distances
Measure the perpendicular distance of the table lamp from the front edge (our x-axis). Let this distance be $a$ cm.
Measure the perpendicular distance of the table lamp from the left edge (our y-axis). Let this distance be $b$ cm.
Step 3: Describe the Position
Now, you can describe the position of the lamp using these two distances, similar to coordinates $(x, y)$. If we take the distance from the front edge as the x-coordinate and the distance from the left edge as the y-coordinate, the position can be described as $(a, b)$.
For example, you could say: "Imagine the front edge is the bottom line and the left edge is the side line. The lamp is located $a$ cm from the front edge and $b$ cm from the left edge."
A more standard way, following the coordinate system idea, would be to mention the distance from the left edge first (like the x-coordinate, movement along the front edge) and then the distance from the front edge (like the y-coordinate, movement along the left edge). So the position could be described as $(b, a)$.
For instance, if the lamp is 30 cm from the left edge and 20 cm from the front edge, you would say: "The lamp is 30 cm along from the left edge and 20 cm up from the front edge."
This method, using two perpendicular reference lines and measuring distances from them, uniquely specifies the position of the table lamp on the study table.
Question 2. (Street Plan) : A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North - South direction and 5th in the East - West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
(i) how many cross - streets can be referred to as (4, 3).
(ii) how many cross - streets can be referred to as (3, 4).
Answer:
We can represent the city plan by drawing a grid. The two main roads can be considered as the x-axis and y-axis. The streets running North-South will be lines parallel to the y-axis, and the streets running East-West will be lines parallel to the x-axis.
There are 5 streets in each direction, and they are 200 m apart. The scale is 1 cm = 200 m. So, in our drawing, the parallel streets will be 1 cm apart.
We can number the North-South streets as 1, 2, 3, 4, 5, starting from the west to the east. Similarly, we can number the East-West streets as 1, 2, 3, 4, 5, starting from the south to the north.
A cross-street is the point where a North-South street and an East-West street intersect. The convention for referring to a cross-street is given as $(N, E)$, where $N$ is the number of the North-South street and $E$ is the number of the East-West street.
(i) How many cross-streets can be referred to as (4, 3).
The cross-street referred to as (4, 3) means the intersection of:
- The 4th street running in the North-South direction.
- The 3rd street running in the East-West direction.
In our model, the 4th North-South street is a specific vertical line, and the 3rd East-West street is a specific horizontal line.
In a coordinate grid system, the intersection of a specific vertical line and a specific horizontal line is always a single, unique point.
Therefore, there is only one cross-street that is the intersection of the 4th North-South street and the 3rd East-West street.
Number of cross-streets referred to as (4, 3) = 1.
(ii) How many cross-streets can be referred to as (3, 4).
The cross-street referred to as (3, 4) means the intersection of:
- The 3rd street running in the North-South direction.
- The 4th street running in the East-West direction.
In our model, the 3rd North-South street is a specific vertical line, and the 4th East-West street is a specific horizontal line.
The intersection of these two specific lines is a single, unique point in the city plan.
Number of cross-streets referred to as (3, 4) = 1.
Conclusion:
The system of referring to cross-streets using ordered pairs $(N, E)$ is similar to using coordinates to locate points on a graph. Each unique ordered pair $(N, E)$ corresponds to exactly one intersection point in the city plan.
(i) There is only one cross-street that can be referred to as (4, 3).
(ii) There is only one cross-street that can be referred to as (3, 4).
Note that the cross-street (4, 3) is different from the cross-street (3, 4), just like the point (4, 3) is different from the point (3, 4) in a coordinate system.
Example 1 & 2 (Before Exercise 3.2)
Example 1. See the Fig. 3.11 and complete the following statements:
(i) The abscissa and the ordinate of the point B are _ _ _ and _ _ _, respectively. Hence, the coordinates of B are (_ _, _ _).
(ii) The x-coordinate and the y-coordinate of the point M are _ _ _ and _ _ _, respectively. Hence, the coordinates of M are (_ _, _ _).
(iii) The x-coordinate and the y-coordinate of the point L are _ _ _ and _ _ _, respectively. Hence, the coordinates of L are (_ _, _ _).
(iv) The x-coordinate and the y-coordinate of the point S are _ _ _ and _ _ _, respectively. Hence, the coordinates of S are (_ _, _ _).

Answer:
Referring to the figure Fig. 3.11:
(i) For point B:
The distance of point B from the y-axis (its perpendicular distance to the y-axis) is 4 units. This is the x-coordinate or abscissa.
The distance of point B from the x-axis (its perpendicular distance to the x-axis) is 3 units. This is the y-coordinate or ordinate.
So, the abscissa and the ordinate of the point B are 4 and 3, respectively. Hence, the coordinates of B are (4, 3).
(ii) For point M:
The x-coordinate of point M is its perpendicular distance from the y-axis. From the figure, M is 3 units to the left of the y-axis, so the x-coordinate is -3.
The y-coordinate of point M is its perpendicular distance from the x-axis. From the figure, M is 4 units above the x-axis, so the y-coordinate is 4.
The x-coordinate and the y-coordinate of the point M are -3 and 4, respectively. Hence, the coordinates of M are (-3, 4).
(iii) For point L:
The distance of point L from the y-axis is 5 units to the left of the origin, so the x-coordinate is -5.
The distance of point L from the x-axis is 4 units below the origin, so the y-coordinate is -4.
The x-coordinate and the y-coordinate of the point L are -5 and -4, respectively. Hence, the coordinates of L are (-5, -4).
(iv) For point S:
The x-coordinate of point S is its perpendicular distance from the y-axis. From the figure, S is 3 units to the right of the y-axis, so the x-coordinate is 3.
The y-coordinate of point S is its perpendicular distance from the x-axis. From the figure, S is 4 units below the x-axis, so the y-coordinate is -4.
The x-coordinate and the y-coordinate of the point S are 3 and -4, respectively. Hence, the coordinates of S are (3, -4).
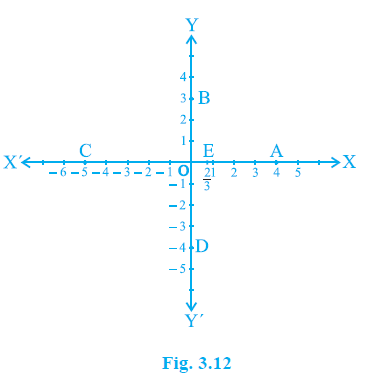
Example 2. Write the coordinates of the points marked on the axes in Fig. 3.12.
Answer:
We need to find the coordinates of the points marked on the axes in Fig. 3.12.
Remember that for any point on the x-axis, its y-coordinate is 0. For any point on the y-axis, its x-coordinate is 0.
(i) Point A:
Point A is on the positive x-axis. Its distance from the y-axis is 4 units to the right of the origin.
Since it is on the x-axis, its distance from the x-axis is 0.
Therefore, the x-coordinate of A is 4 and the y-coordinate of A is 0.
The coordinates of point A are (4, 0).
(ii) Point B:
Point B is on the positive y-axis. Since it is on the y-axis, its distance from the y-axis is 0.
Its distance from the x-axis is 3 units above the origin.
Therefore, the x-coordinate of B is 0 and the y-coordinate of B is 3.
The coordinates of point B are (0, 3).
(iii) Point C:
Point C is on the negative x-axis. Its distance from the y-axis is 5 units to the left of the origin.
Since it is on the x-axis, its distance from the x-axis is 0.
Therefore, the x-coordinate of C is -5 and the y-coordinate of C is 0.
The coordinates of point C are (-5, 0).
(iv) Point D:
Point D is on the negative y-axis. Since it is on the y-axis, its distance from the y-axis is 0.
Its distance from the x-axis is 4 units below the origin.
Therefore, the x-coordinate of D is 0 and the y-coordinate of D is -4.
The coordinates of point D are (0, -4).
(v) Point E:
Point E is on the positive x-axis. Its distance from the y-axis appears to be at $\frac{2}{3}$ units to the right of the origin based on the marking.
Since it is on the x-axis, its distance from the x-axis is 0.
Therefore, the x-coordinate of E is $\frac{2}{3}$ and the y-coordinate of E is 0.
The coordinates of point E are ($\frac{2}{3}$, 0).
Exercise 3.2
Question 1. Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
Answer:
Here are the answers to the given questions about the Cartesian plane:
(i) The name of the horizontal line drawn to determine the position of any point in the Cartesian plane is the x-axis.
The name of the vertical line drawn to determine the position of any point in the Cartesian plane is the y-axis.
(ii) The plane formed by these two lines (the x-axis and the y-axis) is divided into four parts. Each part is called a quadrant.
(iii) The point where the horizontal and vertical lines (the x-axis and the y-axis) intersect is called the origin.
Question 2. See Fig.3.14, given below, and write the following:
(i) The coordinates of B.
(ii) The coordinates of C.
(iii) The point identified by the coordinates (–3, –5).
(iv) The point identified by the coordinates (2, – 4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii) The coordinates of the point M.

Answer:
Referring to the figure Fig. 3.14, let's find the requested coordinates and points.
(i) The coordinates of B:
To find the coordinates of point B, we look at its position relative to the x and y axes. Point B is located 5 units to the left of the y-axis and 2 units above the x-axis.
So, the x-coordinate (abscissa) is -5, and the y-coordinate (ordinate) is 2.
The coordinates of B are (-5, 2).
(ii) The coordinates of C:
To find the coordinates of point C, we look at its position relative to the x and y axes. Point C is located 5 units to the right of the y-axis and 5 units below the x-axis.
So, the x-coordinate is 5, and the y-coordinate is -5.
The coordinates of C are (5, -5).
(iii) The point identified by the coordinates (–3, –5):
To find the point with coordinates (-3, -5), we start at the origin. We move 3 units to the left along the x-axis (because the x-coordinate is -3). Then, from there, we move 5 units downwards parallel to the y-axis (because the y-coordinate is -5).
Locating this point on the graph, we find it corresponds to point E.
(iv) The point identified by the coordinates (2, – 4):
To find the point with coordinates (2, -4), we start at the origin. We move 2 units to the right along the x-axis (because the x-coordinate is 2). Then, from there, we move 4 units downwards parallel to the y-axis (because the y-coordinate is -4).
Locating this point on the graph, we find it corresponds to point G.
(v) The abscissa of the point D:
The abscissa of a point is its x-coordinate. To find the abscissa of point D, we look at its position along the x-axis. Point D is located 6 units to the right of the y-axis.
The abscissa of the point D is 6.
(vi) The ordinate of the point H:
The ordinate of a point is its y-coordinate. To find the ordinate of point H, we look at its position along the y-axis. Point H is located 3 units below the x-axis.
The ordinate of the point H is -3.
(vii) The coordinates of the point L:
Point L is located on the positive y-axis. For any point on the y-axis, the x-coordinate is 0. Point L is 5 units above the x-axis.
So, the x-coordinate is 0, and the y-coordinate is 5.
The coordinates of the point L are (0, 5).
(viii) The coordinates of the point M:
Point M is located on the negative x-axis. For any point on the x-axis, the y-coordinate is 0. Point M is 3 units to the left of the y-axis.
So, the x-coordinate is -3, and the y-coordinate is 0.
The coordinates of the point M are (-3, 0).

